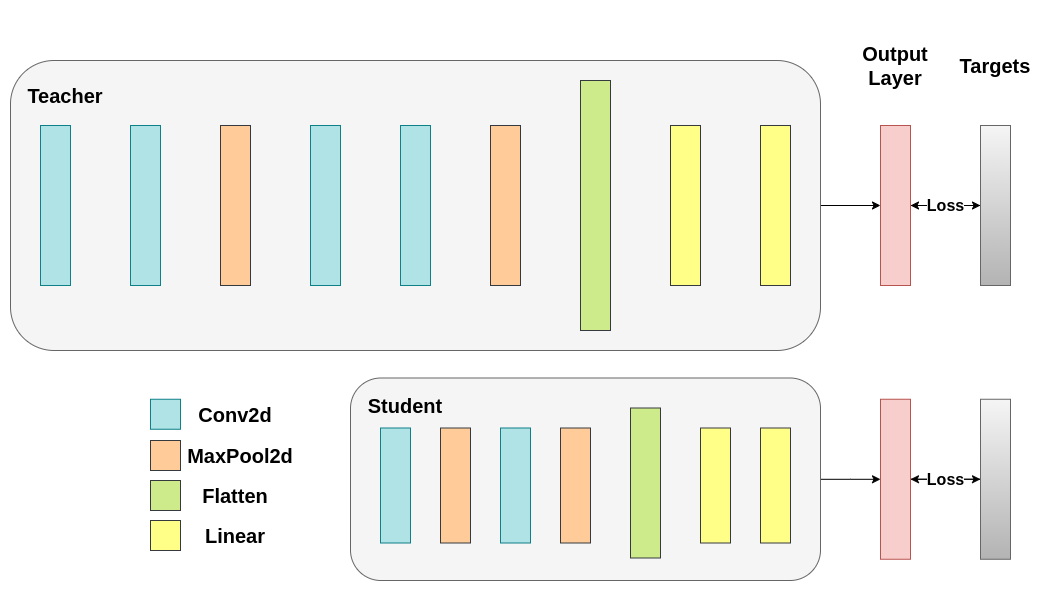
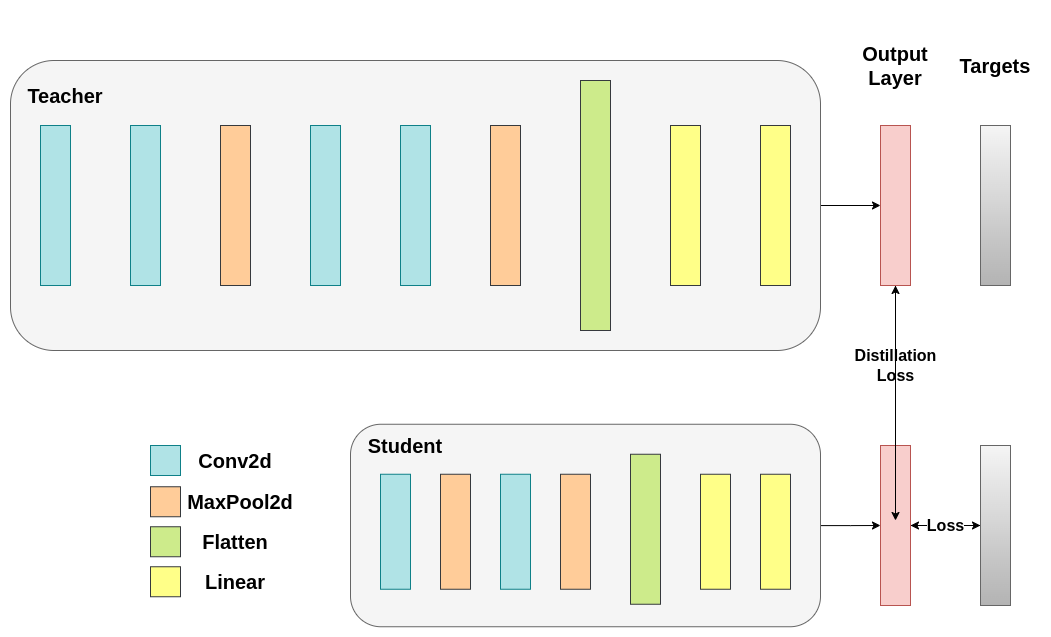
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
| class ModifiedDeepNNCosine(nn.Module):
def __init__(self, num_classes=10):
super(ModifiedDeepNNCosine, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 128, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(128, 64, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(64, 64, kernel_size=3, padding=1),
nn.ReLU(),
nn.Conv2d(64, 32, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
)
self.classifier = nn.Sequential(
nn.Linear(2048, 1024),
nn.ReLU(),
nn.Dropout(0.1),
nn.Linear(1024, 256),
nn.ReLU(),
nn.Dropout(0.1),
nn.Linear(256, num_classes)
)
def forward(self, x):
x = self.features(x)
flattened_conv_output = torch.flatten(x, 1)
x = self.classifier(flattened_conv_output)
flattened_conv_output_after_pooling = torch.nn.functional.avg_pool1d(flattened_conv_output, 2)
return x, flattened_conv_output_after_pooling
class ModifiedLightNNCosine(nn.Module):
def __init__(self, num_classes=10):
super(ModifiedLightNNCosine, self).__init__()
self.features = nn.Sequential(
nn.Conv2d(3, 16, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
nn.Conv2d(16, 16, kernel_size=3, padding=1),
nn.ReLU(),
nn.MaxPool2d(kernel_size=2, stride=2),
)
self.classifier = nn.Sequential(
nn.Linear(1024, 256),
nn.ReLU(),
nn.Dropout(0.1),
nn.Linear(256, num_classes)
)
def forward(self, x):
x = self.features(x)
flattened_conv_output = torch.flatten(x, 1)
x = self.classifier(flattened_conv_output)
return x, flattened_conv_output
modified_nn_deep = ModifiedDeepNNCosine(num_classes=10).to(device)
modified_nn_deep.load_state_dict(nn_deep.state_dict())
print("Norm of 1st layer for deep_nn:", torch.norm(nn_deep.features[0].weight).item())
print("Norm of 1st layer for modified_deep_nn:", torch.norm(modified_nn_deep.features[0].weight).item())
torch.manual_seed(42)
modified_nn_light = ModifiedLightNNCosine(num_classes=10).to(device)
print("Norm of 1st layer:", torch.norm(modified_nn_light.features[0].weight).item())
|