AMP - Automatic Mixed Precision

torch.amp 提供了用于混合精度训练的便捷方法，其中一部分操作使用 torch.float32（即 float）数据类型，另一部分操作则使用较低精度的浮点类型（lower_precision_fp），如 torch.float16（half）或 torch.bfloat16。某些操作（例如线性层和卷积）在低精度浮点下运行速度更快，而其他操作（如归约操作）通常需要 float32 提供的更大动态范围。混合精度训练的目标是为每个操作匹配最合适的数据类型，从而在保证数值稳定性的同时提升训练性能。

模型的精度对存储的影响

import torch
from IPython.display import Image
from transformers import AutoModelForCausalLM

model_path = '../data_collection/Qwen2.5-0.5B-Instruct/'

# all float32
model = AutoModelForCausalLM.from_pretrained(model_path)
print(round(model.get_memory_footprint() / (1024**2)))
# all float16
model = AutoModelForCausalLM.from_pretrained(model_path, torch_dtype=torch.float16)
print(round(model.get_memory_footprint() / (1024**2)))

fp32 和 fp16 加载大小分别为 1885 MB 和 942 MB，参数精度降低就可以更好的利用显存。

# Creates some tensors in default dtype (here assumed to be float32)
a_float32 = torch.rand((8, 8), device="cuda")
b_float32 = torch.rand((8, 8), device="cuda")
c_float32 = torch.rand((8, 8), device="cuda")
d_float32 = torch.rand((8, 8), device="cuda")


with torch.amp.autocast('cuda'):
    # torch.mm is on autocast's list of ops that should run in float16.
    # Inputs are float32, but the op runs in float16 and produces float16 output.
    # No manual casts are required.
    e_float16 = torch.mm(a_float32, b_float32)
    print('in autocast', e_float16.dtype, e_float16.device)
    # Also handles mixed input types
    f_float16 = torch.mm(d_float32, e_float16)
    print('in autocast', f_float16.dtype, e_float16.device)

# After exiting autocast, calls f_float16.float() to use with d_float32
g_float32 = torch.mm(d_float32, f_float16.float())
print('out autocast', g_float32.dtype, g_float32.device)

in autocast torch.float16 cuda:0
in autocast torch.float16 cuda:0
out autocast torch.float32 cuda:0

在使用 torch.amp.autocast() 时，自动切换 fp32 至 fp16

fp32 and fp16

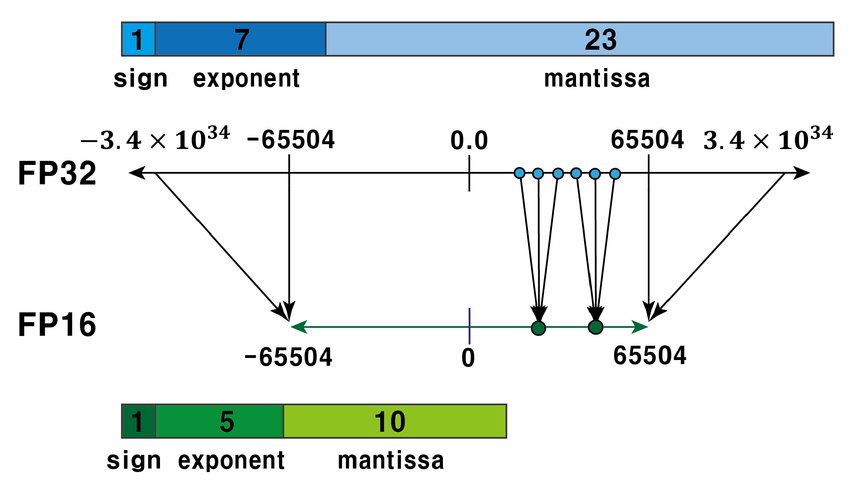
• Sign(符号位): 1 位，0表示整数；1表示负数。
• Exponent(指数位)：5位，简单地来说就是表示整数部分，范围为00001(1)到11110(30)，正常来说整数范围就是 ，但其实为了指数位能够表示负数，引入了一个偏置值，偏置值是一个固定的数，它被加到实际的指数上，在二进制16位浮点数中，偏置值是 15。这个偏置值确保了指数位可以表示从-14到+15的范围即 ，注：当指数位都为00000和11111时，它表示的是一种特殊情况，在IEEE 754标准中叫做非规范化情况。
• Fraction/Mantissa(尾数位)：10位，简单地来说就是表示小数部分，存储的尾数位数为10位，但其隐含了首位的1，实际的尾数精度为11位，这里的隐含位可能有点难以理解，简单通俗来说，假设尾数部分为1001000000，为默认在其前面加一个1，最后变成1.1001000000然后换成10进制就是

正式的计算为

(-1)^sign × 1.fraction × 2^(exponent - bias)

而非正规数（subnormal numbers）的指数部分为 0，此时没有前导 1：

(-1)^sign × 0.fraction × 2^(1 - bias)

fp32 的指数位更多，表示的范围更大，gradient （weight update）的计算需要将其 scale 避免 fp16 的浮点数下溢 (由于数值太小，低于当前类型所能表示的最小的值，计算机就只好把尾数位向右移，空出第一个二进制位)。

fp32 精度和范围更好，fp16 is fast and memory-efficient:

• 更快的 compute throughout （8x）
• 更高的 memory throughout (2x)
• 更小的显存占用 (1/2x)

所以综合两者是更好的策略。

para = torch.tensor([1.], dtype=torch.float32)
update = torch.tensor([.0001], dtype=torch.float32)
print(para + update) # tensor([1.0001])
para = torch.tensor([1.], dtype=torch.float16)
update = torch.tensor([.0001], dtype=torch.float16)
print(para + update) # tensor([1.], dtype=torch.float16)

例如 1. + 0.0001 会导致末位超出范围，而导致被抹去。

混合精度训练

因此 fp16 被用于计算要求没那么高的计算上，而计算要求高的(如loss经常会被reduce到一个值，微调时较小的梯度需要更大的表示范围)则用 fp32。

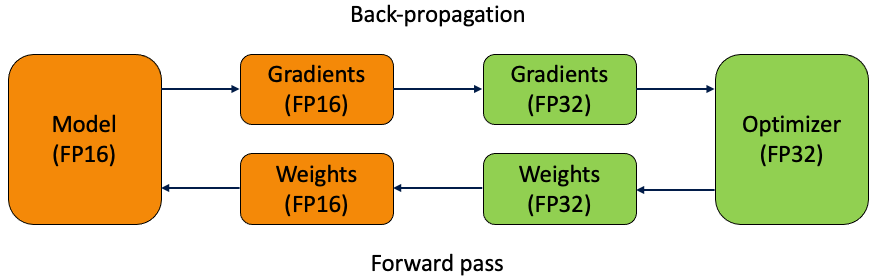
前向时用 fp16 计算，但为了让梯度更新效果更好，将 fp16 的梯度改为 fp32，fp32 的优化器更新后更新 fp32 的模型副本，然后再转换为 fp16 的模型。

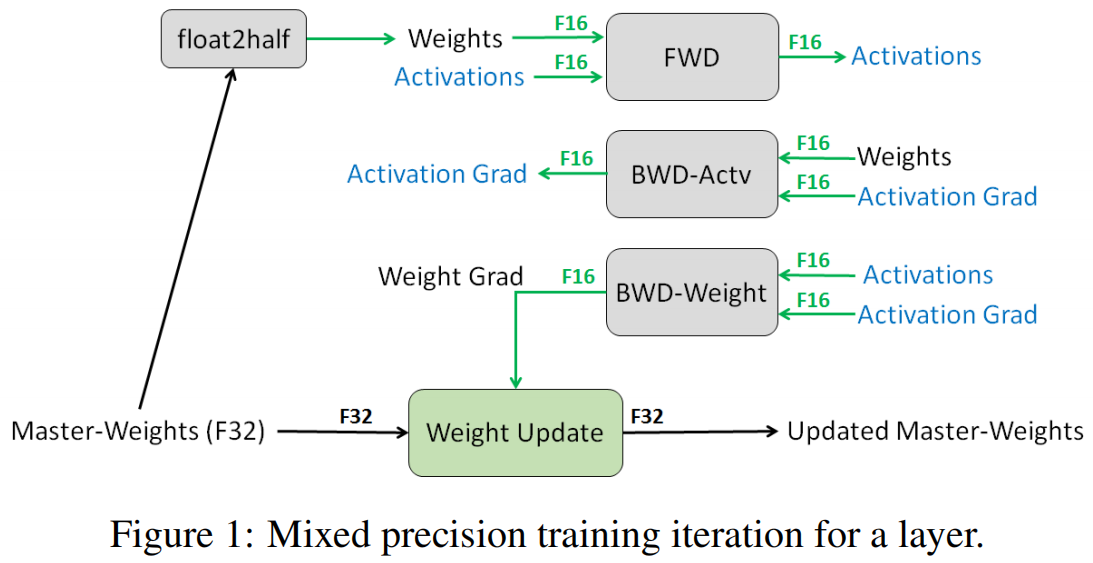
这是混合精度训练文章 https://arxiv.org/pdf/1710.03740.pdf 的示意图，FWD 和 BWD 都是 fp16，只有再更新权重时会用 fp32。

混合精度下的 GPU memory 占用， 个模型参数（fp16）

• Parameters：
• Gradients：
• Optimizer states (Adam, all is fp32) :
  • Parameters copy：
  • Momentum：
  • Variance:：

loss scaling


从图中看出梯度的分布范围，大部分都在 fp16 能表示的范围外面，准确点是小于极小值。这部分如果强行用 fp16 表示，那只能为 0 。

Note that much of the FP16 representable range was left unused, while many values were below the minimum representable range and became zeros. Scaling up the gradients will shift them to occupy more of the representable range and preserve values that are otherwise lost to zeros.

One efficient way to shift the gradient values into FP16-representable range is to scale the loss value computed in the forward pass, prior to starting back-propagation. By chain rule back-propagation ensures that all the gradient values are scaled by the same amount. This requires no extra operations
during back-propagation and keeps the relevant gradient values from becoming zeros.

因此一个方法就是将梯度值 scale 到 fp16 能表达的范围内，只要在 BWD 前把 loss 乘以一个值就可以，梯度都会相同的 scale 。将梯度更新前再反向 scale，当然在 amp 中不需要手动设置。

i.e., 前向传播计算 loss 时将其放大，使得对应的梯度也被同样的放大，能够正常的被 fp16 表示，在更新梯度前再除以 scale。

model = Net().cuda()
optimizer = optim.SGD(model.parameters(), ...)

for input, target in data:
    optimizer.zero_grad()

    # Enables autocasting for the forward pass (model + loss)
    with torch.autocast(device_type="cuda"):
        output = model(input)
        loss = loss_fn(output, target)

    # Exits the context manager before backward()
    loss.backward()
    optimizer.step()